Esta actividad está dirigida para los alumnos que asistirán a la visita guiada a Six Flags, para los que no asisten también aparecerá una actividad específica ese día.
Teorema de Tales. Procedimiento 1.
Por medio del teorema de tales podemos calcular la altura de un objeto al cual no podemos acceder fácilmente, esto se hace a partir de la longitud de la sombra proyectada del objeto grande comparada con la sombra y la altura de un objeto pequeño que sí podemos medir.
Ejemplo.
Un árbol proyecta una sombra de 24 metros, en ese mismo momento una persona que está cerca de este árbol, proyecta una sombra de 6 metros y tiene una altura de 1.5 metros. ¿Cuál es la altura del árbol?
Cómo se resuelve.
Primero se ordenan los datos en forma de fracción, la sombra del objeto grande con su altura y la sombra del objeto pequeño con su altura. Así.
Quedarían como numeradores las alturas del edificio y de la persona.
Quedan como denominadores las sombras que proyectan el árbol y la persona.
Posteriormente se multiplica cruzado, en este caso es 24 por 1.5 y el resultado será dividido entre 6.
Nuestro resultado es 6m, que corresponde a la altura del árbol.
Para resolver cualquier problema se utiliza este método. Se debe considerar que si utilizamos la magnitud de metros en un dato, se deben utilizar para todos los demás, de lo contrario el resultado será erróneo.
Teorema de Tales. Procedimiento 2.
Podemos aplicar el teorema de tales utilizando el reflejo de los objetos que deseamos medir y la distancia a la que se encuentra cada cuerpo como lo muestra la siguiente imagen.
En este caso el procedimiento es el mismo, las alturas de los objetos quedan como numeradores y las respectivas distancias como denominadores.
Por lo tanto la altura del árbol es 5.4 metros.
Para efectuar la actividad, el procedimiento que se utilizará es el segundo donde se calculan las distancias desde un punto de reflexión. Se nota el primer procedimiento en caso de que sea más fácil de utilizar recuerda medir bien las distancias.
Actividad. Se debe calcular la altura aproximada de los juegos Boomerang, Rueda India y Kilahuea.
lunes, 30 de noviembre de 2015
miércoles, 25 de noviembre de 2015
B2. Actividad 24. 25/11/15
B2. Actividad 24. 25/11/15
Actividad. Crea los segmentos y los ángulos indicados para cada caso. Las medidas de los segmentos están en centímetros.
Actividad. Crea los segmentos y los ángulos indicados para cada caso. Las medidas de los segmentos están en centímetros.
martes, 24 de noviembre de 2015
B2. Actividad 23. 24/11/15
B2. Actividad 23. 24/11/15
Actividad construye el ángulo indicado utilizando los segmentos y las medidas correspondientes.
Segmento AB 4.5 cm. Ángulo B 45 grados. Segmento BC 3 cm.
Segmento AB 3.5 cm. Ángulo B 25 grados. Segmento BC 3.5 cm.
Segmento AB 2.5 cm. Ángulo B 30 grados. Segmento BC 3 cm.
Segmento AB 4 cm. Ángulo B 55 grados. Segmento BC 3cm.
Segmento AB 5 cm. Ángulo B 65 grados. Segmento BC 3cm.
Segmento AC 8 cm. Ángulo C 40 grados. Segmento BC 3cm.
Segmento AC 7 cm. Ángulo C 65 grados. Segmento BC 3cm.
Segmento AC 9 cm. Ángulo B 35 grados. Segmento BC 3cm.
Actividad construye el ángulo indicado utilizando los segmentos y las medidas correspondientes.
Segmento AB 4.5 cm. Ángulo B 45 grados. Segmento BC 3 cm.
Segmento AB 3.5 cm. Ángulo B 25 grados. Segmento BC 3.5 cm.
Segmento AB 2.5 cm. Ángulo B 30 grados. Segmento BC 3 cm.
Segmento AB 4 cm. Ángulo B 55 grados. Segmento BC 3cm.
Segmento AB 5 cm. Ángulo B 65 grados. Segmento BC 3cm.
Segmento AC 8 cm. Ángulo C 40 grados. Segmento BC 3cm.
Segmento AC 7 cm. Ángulo C 65 grados. Segmento BC 3cm.
Segmento AC 9 cm. Ángulo B 35 grados. Segmento BC 3cm.
lunes, 23 de noviembre de 2015
B2. Actividad 22. 23/11/15
B2. Actividad 22. 23/11/15
Tema. Construcción de ángulos.
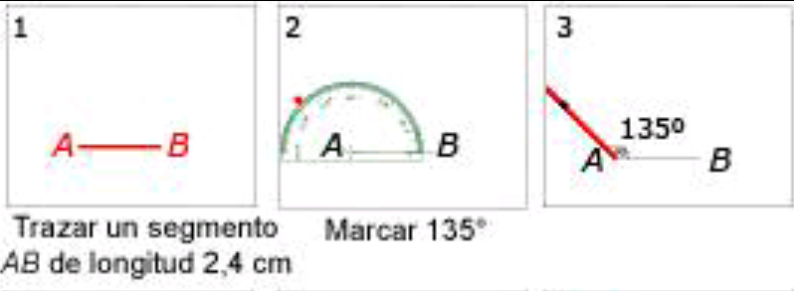
1. Se traza un segmento (línea recta) marcando el punto A y el punto B.
2. coloca tu transportador en el punto A o en el punto B según te indiquen.
3. Cuenta y marca los grados indicados para que te traces una línea desde el vértice que usaste hacia la marca de los grados que contaste.
Observa los ejemplos.
Ángulo de 26 grados desde el punto A.
Ángulo de 135 grados desde el punto A.
Actividad.
1. Crea los siguientes ángulos desde el punto A.
50, 45, 72, 81, 93, 105, 48, 36, 49, 73.
2. Crea los siguientes ángulos desde el punto B.
150, 96, 58, 79, 75, 140, 169, 156, 76, 43.
Tema. Construcción de ángulos.
1. Se traza un segmento (línea recta) marcando el punto A y el punto B.
2. coloca tu transportador en el punto A o en el punto B según te indiquen.
3. Cuenta y marca los grados indicados para que te traces una línea desde el vértice que usaste hacia la marca de los grados que contaste.
Observa los ejemplos.
Ángulo de 26 grados desde el punto A.
Ángulo de 135 grados desde el punto A.
Actividad.
1. Crea los siguientes ángulos desde el punto A.
50, 45, 72, 81, 93, 105, 48, 36, 49, 73.
2. Crea los siguientes ángulos desde el punto B.
150, 96, 58, 79, 75, 140, 169, 156, 76, 43.
viernes, 20 de noviembre de 2015
B2. Actividad 21. 20/11/15
B2. Actividad 21. 20/11/15
Actividad. Crea 6 polígonos irregulares (2 de 4 lados, 2 de 5 lados y 2 de 6 lados). A cada uno anota las medidas de sus ángulos internos.
Actividad. Crea 6 polígonos irregulares (2 de 4 lados, 2 de 5 lados y 2 de 6 lados). A cada uno anota las medidas de sus ángulos internos.
B2. Actividad 20. 20/11/15
B2. Actividad 20. 20/11/15
Actividad. Elabora el formulario del tema polígono. Los subtemas deben ser polígono simple y complejo, polígono regular e irregular, vértice, arista y ángulo.
Actividad. Elabora el formulario del tema polígono. Los subtemas deben ser polígono simple y complejo, polígono regular e irregular, vértice, arista y ángulo.
jueves, 19 de noviembre de 2015
B2. Actividad 19. 19/11/15
B2. Actividad 19. 19/11/15
Para construir un polígono utilizando sus ángulos centrales se debe hacer lo siguiente:
1. Se coloca un punto qué servirá como centro para crear el polígono.
2. Se realizará una división, siempre será 360 grados entre la cantidad de lados del polígono que se desea construir.
3. El resultado de la división será la medida del ángulo central. Con esta medida se coloca el transportador para hacerlas marcas de la medida de los ángulos centrales.
4. Se verificará que sea la misma distancia desde el centro hacia cada marca, por último se unirán los extremos de cada línea marcada y tendremos nuestro polígono.
Ejemplo.
Si quisiera construir un polígono de tres lados, es decir, un triángulo regular, se debe dividir primero 360 entre 3 el resultado será 120, qué es la medida de cada ángulo central del polígono
Paso 1. Se coloca el centro del polígono que en este caso es el punto de color azul.
Paso 2. Se realiza la división que en este caso corresponde a 360 entre 3 el resultado, es 120 grados para cada ángulo central.
Paso 3. Al utilizar el transportador se mide desde 0 hasta 120, para este ejemplo la medida del ángulo central es de 120 grados entre cada línea anaranjada. Asimismo cada línea anaranjada debe tener la misma medida por ejemplo 4 centímetros.
Paso 4. Se unirán los extremos década línea anaranjada, es decir, se unirán los puntos verdes para formar el polígono deseado
Actividad. Construye en tu cuaderno los polígonos de 5 6, 7 y 8 lados. Utiliza tu transportador y regla.
Para construir un polígono utilizando sus ángulos centrales se debe hacer lo siguiente:
1. Se coloca un punto qué servirá como centro para crear el polígono.
2. Se realizará una división, siempre será 360 grados entre la cantidad de lados del polígono que se desea construir.
3. El resultado de la división será la medida del ángulo central. Con esta medida se coloca el transportador para hacerlas marcas de la medida de los ángulos centrales.
4. Se verificará que sea la misma distancia desde el centro hacia cada marca, por último se unirán los extremos de cada línea marcada y tendremos nuestro polígono.
Ejemplo.
Si quisiera construir un polígono de tres lados, es decir, un triángulo regular, se debe dividir primero 360 entre 3 el resultado será 120, qué es la medida de cada ángulo central del polígono
Paso 1. Se coloca el centro del polígono que en este caso es el punto de color azul.
Paso 2. Se realiza la división que en este caso corresponde a 360 entre 3 el resultado, es 120 grados para cada ángulo central.
Paso 3. Al utilizar el transportador se mide desde 0 hasta 120, para este ejemplo la medida del ángulo central es de 120 grados entre cada línea anaranjada. Asimismo cada línea anaranjada debe tener la misma medida por ejemplo 4 centímetros.
Paso 4. Se unirán los extremos década línea anaranjada, es decir, se unirán los puntos verdes para formar el polígono deseado
Actividad. Construye en tu cuaderno los polígonos de 5 6, 7 y 8 lados. Utiliza tu transportador y regla.
miércoles, 18 de noviembre de 2015
B2. Actividad 18. 18/11/15
B2. Actividad 18. 18/11/15
Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.
Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.
B2. Actividad 17. 18/11/15
B2. Actividad 17. 18/11/15
Tema. Polígono regular e irregular.
Polígono regular. Es aquella figura en la que todos sus lados o aristas miden lo mismo y también sus ángulos miden lo mismo.

Polígono irregular. Es aquella figura en la que por lo menos uno de sus lados o aristas es diferente al de los otros, de la misma forma por lo menos uno de sus ángulos tiene diferente medida a los otros.

Nota. Para que se considere un polígono debe estar formado por líneas rectas si alguna línea es curva deja de ser polígono. También todas las líneas deben estar unidas si hay una separación deja de ser polígono.
Actividad. Elabora dos organizadores gráficos del tema polígonos, los subtemas deben ser: partes de un polígono, polígono simple, polígono complejo, polígono regular y polígono irregular.
Tema. Polígono regular e irregular.
Polígono regular. Es aquella figura en la que todos sus lados o aristas miden lo mismo y también sus ángulos miden lo mismo.

Polígono irregular. Es aquella figura en la que por lo menos uno de sus lados o aristas es diferente al de los otros, de la misma forma por lo menos uno de sus ángulos tiene diferente medida a los otros.
Nota. Para que se considere un polígono debe estar formado por líneas rectas si alguna línea es curva deja de ser polígono. También todas las líneas deben estar unidas si hay una separación deja de ser polígono.
Actividad. Elabora dos organizadores gráficos del tema polígonos, los subtemas deben ser: partes de un polígono, polígono simple, polígono complejo, polígono regular y polígono irregular.
B2. Actividad 16. 17/11/15
B2. Actividad 16. 17/11/15
Tema. Partes de un polígono.
Vértice. Es el punto donde se unen dos líneas rectas.
Arista. Es cada una de las líneas rectas de una figura, también conocidas como lado.
Ángulo. Es la medida de separación en grados entre dos aristas.
Tema. Polígonos simples y complejos.
Un polígono simple es aquél en donde ninguno de sus lados se cruza o encima con otro.

Ejemplo de polígono simple, ningún lado se cruza.
Un polígono complejo es aquél en el que por lo menos uno de sus lados o aristas se cruza encima con otra u otras

Ejemplo de polígono complejo, uno de sus lados o aristas se cruza con otro.
Actividad. Construye 10 polígonos simples y 10 polígonos complejos.
Tema. Partes de un polígono.
Vértice. Es el punto donde se unen dos líneas rectas.
Arista. Es cada una de las líneas rectas de una figura, también conocidas como lado.
Ángulo. Es la medida de separación en grados entre dos aristas.
¿Es un polígono?
Los polígonos son formas bidimensionales. Están hechos con líneas rectas, y su forma es "cerrada" (todas las líneas están conectadas).
| Polígono (lados rectos) | No es un polígono (tiene una curva) | No es un polígono (abierto, no cerrado) |
Tema. Polígonos simples y complejos.
Un polígono simple es aquél en donde ninguno de sus lados se cruza o encima con otro.
Ejemplo de polígono simple, ningún lado se cruza.
Un polígono complejo es aquél en el que por lo menos uno de sus lados o aristas se cruza encima con otra u otras
Ejemplo de polígono complejo, uno de sus lados o aristas se cruza con otro.
Actividad. Construye 10 polígonos simples y 10 polígonos complejos.
miércoles, 11 de noviembre de 2015
B2. Actividad 15. 12/11/15
B2. Actividad 15. 12/11/15
Actividad. Elabora el formulario con dos ejemplos del tema:
Actividad. Elabora el formulario con dos ejemplos del tema:
- Proporcionalidad inversa.
B2. Actividad 14. 12/11/15
B2. Actividad 14. 12/11/15
Actividad. Analiza los siguientes grupos de datos y crea un problema de proporcionalidad inversa para cada uno.
Actividad. Analiza los siguientes grupos de datos y crea un problema de proporcionalidad inversa para cada uno.
martes, 10 de noviembre de 2015
B2. Actividad 13. 11/11/15
B2. Actividad 13. 11/11/15
Actividad. Analiza las siguientes situaciones se aplica la proporcionalidad inversa.
Osvaldo tiene 10 vacas y se acaban una carga de alimento en 18.5 días, si llegan 20 vacas más ¿En cuánto tiempo se terminan el alimento?
10 niños se comen un paquete de conchas en 6.5 días, si llegan 5 niños más ¿en cuántos días se las terminarán la misma cantidad de conchas?
Una avioneta viaja a 80 km/h en hacer un viaje de una ciudad a otra tarda 8.4 horas. Si vuelve a hacer el viaje pero tarda 6.7 horas ¿a cuántos kilómetros viajó la segunda ocasión?
En un zoológico el precio es fijo de 400 pesos por cada uno sólo si entrar 40 alumnos, pero si sólo entraron 35 ¿cuánto pagó cada uno?
15 vacas consumen un depósito de alimento en 11 días. Si llegan 9 vacas más ¿En cuántos días se comen el alimento?
Un auto que circula a 104Km/h. invierte 5.5 horas en cubrir la distancia que separa dos ciudades, si vuelve a realizar el viaje y emplea 7.3 horas. ¿A qué velocidad circula en el segundo viaje?
Una grupo de 13 obreros realiza una construcción en 15.5 días. ¿Cuántos obreros se necesitan para hacer el mismo trabajo en 8 días?
Una barco que viaja a 97Km/h. invierte 2.5 días en cubrir una distancia, si vuelve a realizar el viaje y emplea 3.5 días. ¿A qué velocidad viajaba en la segunda ocasión?
Actividad. Analiza las siguientes situaciones se aplica la proporcionalidad inversa.
Osvaldo tiene 10 vacas y se acaban una carga de alimento en 18.5 días, si llegan 20 vacas más ¿En cuánto tiempo se terminan el alimento?
10 niños se comen un paquete de conchas en 6.5 días, si llegan 5 niños más ¿en cuántos días se las terminarán la misma cantidad de conchas?
Una avioneta viaja a 80 km/h en hacer un viaje de una ciudad a otra tarda 8.4 horas. Si vuelve a hacer el viaje pero tarda 6.7 horas ¿a cuántos kilómetros viajó la segunda ocasión?
En un zoológico el precio es fijo de 400 pesos por cada uno sólo si entrar 40 alumnos, pero si sólo entraron 35 ¿cuánto pagó cada uno?
15 vacas consumen un depósito de alimento en 11 días. Si llegan 9 vacas más ¿En cuántos días se comen el alimento?
Un auto que circula a 104Km/h. invierte 5.5 horas en cubrir la distancia que separa dos ciudades, si vuelve a realizar el viaje y emplea 7.3 horas. ¿A qué velocidad circula en el segundo viaje?
Una grupo de 13 obreros realiza una construcción en 15.5 días. ¿Cuántos obreros se necesitan para hacer el mismo trabajo en 8 días?
Una barco que viaja a 97Km/h. invierte 2.5 días en cubrir una distancia, si vuelve a realizar el viaje y emplea 3.5 días. ¿A qué velocidad viajaba en la segunda ocasión?
lunes, 9 de noviembre de 2015
B2. Actividad 12. 10/11/15
B2. Actividad 12. 10/11/15
Actividad. Resuelve los siguientes problemas aplicando la proporcionalidad inversa.
12 borregos consumen un depósito de alimento en 8 días. Si llegan 12 borregos más ¿En cuántos días se comen el alimento?
Una motocicleta que circula a 110Km/h. invierte 11 horas en cubrir la distancia que separa dos ciudades, si vuelve a realizar el viaje y emplea 10 horas. ¿A qué velocidad circula en el segundo viaje?
Una cuadrilla formada por 8 obreros realiza una construcción en 7 días. ¿Cuántos obreros se necesitan para hacer el mismo trabajo en 8 días?
Una avioneta que viaja a 100Km/h. invierte 7 horas en cubrir la distancia que separa dos ciudades, si vuelve a realizar el viaje y emplea 4 horas. ¿A qué velocidad viajaba en la segunda ocasión?
En una granja 200 gallinas consumen un depósito de alimento que en 15 días. ¿Cuánto tiempo demorarán 300 gallinas terminar la misma cantidad de alimento? 10 días
Un grupo de alumnos entrará a un parque de diversiones a un precio fijo, si son 32 alumnos cada uno pagaría $400, pero si al final sólo entran 25 alumnos ¿cuánto pagaría cada uno?
Para levantar una pared en una casa, se ha conformado una cuadrilla de 6 obreros. Culminar con dicha tarea les llevó un total de 4 horas. ¿Cuántos obreros más hubieran hecho falta para hacer similar trabajo en un total de 3 horas?
Actividad. Resuelve los siguientes problemas aplicando la proporcionalidad inversa.
12 borregos consumen un depósito de alimento en 8 días. Si llegan 12 borregos más ¿En cuántos días se comen el alimento?
Una motocicleta que circula a 110Km/h. invierte 11 horas en cubrir la distancia que separa dos ciudades, si vuelve a realizar el viaje y emplea 10 horas. ¿A qué velocidad circula en el segundo viaje?
Una cuadrilla formada por 8 obreros realiza una construcción en 7 días. ¿Cuántos obreros se necesitan para hacer el mismo trabajo en 8 días?
Una avioneta que viaja a 100Km/h. invierte 7 horas en cubrir la distancia que separa dos ciudades, si vuelve a realizar el viaje y emplea 4 horas. ¿A qué velocidad viajaba en la segunda ocasión?
En una granja 200 gallinas consumen un depósito de alimento que en 15 días. ¿Cuánto tiempo demorarán 300 gallinas terminar la misma cantidad de alimento? 10 días
Un grupo de alumnos entrará a un parque de diversiones a un precio fijo, si son 32 alumnos cada uno pagaría $400, pero si al final sólo entran 25 alumnos ¿cuánto pagaría cada uno?
Para levantar una pared en una casa, se ha conformado una cuadrilla de 6 obreros. Culminar con dicha tarea les llevó un total de 4 horas. ¿Cuántos obreros más hubieran hecho falta para hacer similar trabajo en un total de 3 horas?
B2. Actividad 11. 9/11/15
B2. Actividad 11. 9/11/15
Tema. Proporcionalidad inversa.
La proporcionalidad es la relación que existe entre dos cantidades.
La proporcionalidad inversa indica que si una cantidad aumenta la otra disminuye o si una cantidad disminuye la otra aumenta.
Ejemplo.
José y un compañero pintan una casa en 12 días, si invitaran a otras dos personas a trabajar ¿Cuántos días tardarían en pintar la casa?
Paso 1.
Se ordenan los datos.
Paso 2.
Se realiza un despeje, esto significa que el dato que está solo quedará como divisor.
Paso 3.
Se realiza la multiplicación y la división correspondientes. El resultado será el dato que hace falta.
Nota. Sin importar que dato haga falta siempre se realiza este proceso.
Actividad. Resuelve los siguientes problemas aplicando la proporcionalidad inversa.
En un establo 12 caballos consumen una carga de alimento en 9 días. Si llegan seis caballos más ¿En cuántos días se comerían la misma cantidad de alimento?
Un grupo de personas contrató un autobús a un precio fijo para un viaje, al principio viajarían 44 personas y el precio para cada uno sería de 9 peso, pero finalmente viajaron 36 ¿cuánto tendría que pagar cada uno?
Un coche que circula a 70 kilómetros por hora tarda 9 horas en cubrir una distancia entre dos ciudades, si vuelve a realizar el mismo viaje pero tarda 5 horas ¿A qué velocidad circulaba en el segundo viaje?
4 llaves de agua llenar un depósito en 10 horas. Si usáramos 8 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
Dos llaves llenan un depósito en 5 horas, si se usarán 10 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
Tema. Proporcionalidad inversa.
La proporcionalidad es la relación que existe entre dos cantidades.
La proporcionalidad inversa indica que si una cantidad aumenta la otra disminuye o si una cantidad disminuye la otra aumenta.
Ejemplo.
José y un compañero pintan una casa en 12 días, si invitaran a otras dos personas a trabajar ¿Cuántos días tardarían en pintar la casa?
Paso 1.
Se ordenan los datos.
Paso 2.
Se realiza un despeje, esto significa que el dato que está solo quedará como divisor.
Paso 3.
Se realiza la multiplicación y la división correspondientes. El resultado será el dato que hace falta.
Nota. Sin importar que dato haga falta siempre se realiza este proceso.
Actividad. Resuelve los siguientes problemas aplicando la proporcionalidad inversa.
En un establo 12 caballos consumen una carga de alimento en 9 días. Si llegan seis caballos más ¿En cuántos días se comerían la misma cantidad de alimento?
Un grupo de personas contrató un autobús a un precio fijo para un viaje, al principio viajarían 44 personas y el precio para cada uno sería de 9 peso, pero finalmente viajaron 36 ¿cuánto tendría que pagar cada uno?
Un coche que circula a 70 kilómetros por hora tarda 9 horas en cubrir una distancia entre dos ciudades, si vuelve a realizar el mismo viaje pero tarda 5 horas ¿A qué velocidad circulaba en el segundo viaje?
4 llaves de agua llenar un depósito en 10 horas. Si usáramos 8 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
Dos llaves llenan un depósito en 5 horas, si se usarán 10 llaves para el mismo depósito ¿cuánto tiempo tardaría en llenarlo?
jueves, 5 de noviembre de 2015
B2. Actividad 10. 6/11/15
B2. Actividad 10. 6/11/15
Actividad. Elabora el formulario del tema proporcionalidad directa. Anota 2 ejemplos.
Actividad. Elabora el formulario del tema proporcionalidad directa. Anota 2 ejemplos.
B2. Actividad 9. 6/11/15
B2. Actividad 9. 6/11/15
Actividad. Calcula la proporcionalidad directa de las siguientes situaciones.
Juan compró dos pantalones, que costaron $340, ¿cuál sería el costo si compra 2, 4, 8, 10?
Luisa compró 3 playeras que costaron $150, ¿cuánto tendría que pagar si comprará 2, 6, 10 y 12 playeras?
María compró 2 chocolates que costaron $15, si comprara 6, 15, 20 y 25 ¿cuánto pagaría?
Actividad. Calcula la proporcionalidad directa de las siguientes situaciones.
Juan compró dos pantalones, que costaron $340, ¿cuál sería el costo si compra 2, 4, 8, 10?
Luisa compró 3 playeras que costaron $150, ¿cuánto tendría que pagar si comprará 2, 6, 10 y 12 playeras?
María compró 2 chocolates que costaron $15, si comprara 6, 15, 20 y 25 ¿cuánto pagaría?
B2. Actividad 8. 5/11/15
B2. Actividad 8. 5/11/15
Actividad. Calcula la proporcionalidad directa de las siguientes situaciones.
Carlos compró un par de tenis, que cuestan $280, ¿cuál sería el costo si compra 2, 4, 8, 10?
María compró una chamarra que costaba $340, ¿cuánto tendría que pagar si comprará 2, 6, 10 y 12 chamarras?
Pedro compró donas que costaban $15 cada una, si compró 6, 15, 20 y 25 ¿cuánto pagó?
Juan compró una bolsa que cuesta $120, ¿cuál sería el costo si comprará 2, 5, 10 y 15 bolsas?
Actividad. Calcula la proporcionalidad directa de las siguientes situaciones.
Carlos compró un par de tenis, que cuestan $280, ¿cuál sería el costo si compra 2, 4, 8, 10?
María compró una chamarra que costaba $340, ¿cuánto tendría que pagar si comprará 2, 6, 10 y 12 chamarras?
Pedro compró donas que costaban $15 cada una, si compró 6, 15, 20 y 25 ¿cuánto pagó?
Juan compró una bolsa que cuesta $120, ¿cuál sería el costo si comprará 2, 5, 10 y 15 bolsas?
miércoles, 4 de noviembre de 2015
B2. Actividad 7. 4/11/15
B2. Actividad 7. 4/11/15
Actividad. Analiza las siguientes situaciones y aplica la proporcionalidad directa para cada una.
Marco compró productos para su tienda, el precio de tres detergentes es de 126.5 ¿cuál sería el precio de 4, 5, 9, 12, 15, 21 y 27 unidades?
Viridiana comprará playeras cada una cuesta 10 pesos y necesita 14. ¿cuál sería el costo para cada cantidad entre 1 y 14?
Actividad. Analiza las siguientes situaciones y aplica la proporcionalidad directa para cada una.
Marco compró productos para su tienda, el precio de tres detergentes es de 126.5 ¿cuál sería el precio de 4, 5, 9, 12, 15, 21 y 27 unidades?
Viridiana comprará playeras cada una cuesta 10 pesos y necesita 14. ¿cuál sería el costo para cada cantidad entre 1 y 14?
B2. Actividad 6. 4/11/15
B2. Actividad 6. 4/11/15
Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.
Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.
martes, 3 de noviembre de 2015
B2. Actividad 5. 3/11/15
B2. Actividad 5. 3/11/15
Tema. Proporcionalidad directa.
M
La proporcionalidad es una relación que existe entre dos cantidades.
En el caso de la proporcionalidad directa la relación es que: si la primer cantidad aumenta la segunda también lo hace.
Ejemplo.
Luis comprará pintura, cada litro tiene un precio de 75 pesos si necesita 15 litros ¿Cuál será el costo total?
Para calcular cualquier situación de proporcionalidad directa se tiene que utilizar una regla de tres.
Se multiplican las cantidades cruzadas y el resultado se divide entre la tercer cantidad.
Actividad. Resuelve las siguientes situaciones calculando la proporcionalidad directa.
Carlos comprará pintura, un litro cuesta 45 pesos, si comprará las siguientes cantidades 2, 3, 6, 11, 16, 21, 35 y 42 cuánto pagará.
Tema. Proporcionalidad directa.
M
La proporcionalidad es una relación que existe entre dos cantidades.
En el caso de la proporcionalidad directa la relación es que: si la primer cantidad aumenta la segunda también lo hace.
Ejemplo.
Luis comprará pintura, cada litro tiene un precio de 75 pesos si necesita 15 litros ¿Cuál será el costo total?
Para calcular cualquier situación de proporcionalidad directa se tiene que utilizar una regla de tres.
Se multiplican las cantidades cruzadas y el resultado se divide entre la tercer cantidad.
Actividad. Resuelve las siguientes situaciones calculando la proporcionalidad directa.
Carlos comprará pintura, un litro cuesta 45 pesos, si comprará las siguientes cantidades 2, 3, 6, 11, 16, 21, 35 y 42 cuánto pagará.
Suscribirse a:
Comentarios (Atom)