B3. Actividad 5. 16/12/15

B3. Actividad 5. 16/12/15

Actividad. Calcula el área de las siguientes figuras aplica correctamente la fórmula para cada una.

Cuadrado. 3.5cm
Cuadrado. 7.5cm

Rectángulo. Base 17cm, altura 23cm
Rectángulo. Base 43cm, altura 79cm

Triángulo. Base 12.4cm, altura 17.1cm
Triángulo. Base 11.6cm, altura 7.4cm

Rombo. Diagonal mayor 23cm, diagonal menor 14cm
Rombo. Diagonal mayor 15.2cm, diagonal menor 10.9cm

Romboide. Base 4.6cm, altura 5.3cm

Romboide. Base 8.5cm, altura 1.4cm

Trapecio. Base mayor 4cm, base menor 2.5cm, altura 3cm

Trapecio. Base mayor 2.5cm, base menor 2.1cm, altura 1.5 cm

Círculo. Radio 13.4cm

Círculo. Radio 21.2cm

Pentágono. Lado 5cm, apotema 3.5cm
Pentágono. Lado 6cm, apotema 5.5cm

B3. Actividad 4. 15/12/15

B3. Actividad 4. 15/12/15


Tema. Áreas.

El área es la medida de una superficie en unidades cuadradas (mm², cm², m², km², etc.).

El resultado al calcular una área se puede interpretar como la cantidad de cuadros que caben en la superficie de una figura.


Ejemplo 1.

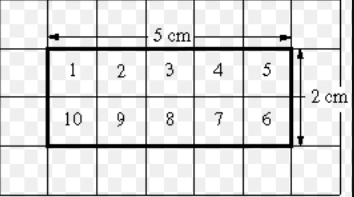
Si tengo un rectángulo que mide 5cm de base por 2cm de altura. Su área es 10 cm².

Eso significa que dentro de ese rectángulo  caben 10 cuadrados que miden un centímetro de cada lado.

Ejemplo 2.

En este ejemplo ocurre lo mismo el cuadrado tiene 4 centímetros de lado, por lo tanto su área será 16cm ²


Ejemplo 3.

En este último ejemplo podemos observar que el área es de un centímetro cuadrado (la de color rojo), sin embargo, podemos marcar el área en milímetros (de color azul).


Para calcular el área se debe conocer la fórmula de cada figura.

Área de un triángulo

Área de un cuadrado

Área de un rectángulo

Área de un rombo

Área del romboide

A = b · h

Área del trapecio

Área de un polígono regular

Área de un polígono

El área se obtienetriangulando el polígono ysumando el área de dichos triángulos.

A = T ₁ + T ₂ + T ₃ + T ₄

Área de un círculo

Actividad. Completa el siguiente cuadro anotando la fórmula para calcular el área de las figuras y dos ejemplo en cada una.

Usa las siguientes medidas para los ejemplos.

Cuadrado. 8cm
Cuadrado. 25cm

Rectángulo. Base 30cm, altura 50cm
Rectángulo. Base 40cm, altura 60cm

Triángulo. Base 35cm, altura 40cm
Triángulo. Base 60cm, altura 30cm

Rombo. Diagonal mayor 48cm, diagonal menor 38cm
Rombo. Diagonal mayor 70cm, diagonal menor 50cm

Romboide. Base 64cm, altura 35cm

Romboide. Base 58cm, altura 41cm

Trapecio. Base mayor 40cm, base menor 25cm, altura 30cm

Trapecio. Base mayor 25cm, base menor 20cm, altura 15 cm

Círculo. Radio 20cm

Círculo. Radio 15cm

Pentágono. Lado 50cm, apotema 30cm
Pentágono. Lado 15cm, apotema 13cm

B3. Actividad 3. 14/12/15

B3. Actividad 3. 14/12/15

Tema. Cálculo del perímetro.

El perímetro es la suma de todas las medidas de los lados de una figura.


Para obtenerlo se suman todos los lados sin olvidar colocar la magnitud indicada (es decir, si son cm, m, km,etc.)


Ejemplo.

Cuál es el perímetro de las siguientes figuras.

10+10+10+10+3+7+4+5= 59 cm

6+5+6+5= 22cm

Actividad. Crea 10 polígonos simples irregulares, mide y anota sus lados, además de obtener el perímetro para cada una.

B3. Actividad 2. 14/12/15

B3. Actividad 2. 14/12/15

Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.

B3. Actividad 1. 14/12/15

B3. Actividad 1. 14/12/15

Actividad. Elabora la carátula correspondiente al tercer bimestre. Los datos qu e debe incluir son:


Nombre.
Asignatura.
Grado.
Grupo.
Bimestre.

B2. Actividad 31. 8/12/15

B2. Actividad 31. 8/12/15

Actividad. Elabora un organizador gráfico de los temas:

1. Cómo medir un ángulo interno.
2. Cómo medir un ángulo externo.
3. Cómo construir un polígono regular desde su ángulo central.

B2. Actividad 30. 7/12/15

B2. Actividad 30. 7/12/15

Actividad.  Construye 6 polígonos irregulares y a cada uno marca sus ángulos internos y externos.

B2. Actividad 29. 4/12/15

B2. Actividad 29. 4/12/15

Actividad. Elabora el formulario, usando un cuadro de triple entrada, para cada tema deben ser dos ejemplos, los temas deben ser:

1. Cálculo de la medida del ángulo externo de un polígono.
2. Cálculo de la medida del ángulo interno de un polígono.
3. Cálculo de la medida del ángulo central de un polígono.

B2. Actividad 28. 3/11/15

B2. Actividad 28. 3/11/15


Tema. Creación de polígonos a partir de su ángulo central.

Los pasos para crear un polígono desde su ángulo central son:

1. Se marca un punto que servirá de centro en nuestra figura.
2. Se dividirá 360 entre la cantidad de lados que tendrá nuestro polígono regular.
3. El resultado de esta división será la medida del ángulo central de acuerdo a la cantidad se realizarán las marcas que serán los vértices en nuestra figura.
4. Las marcas se unirán cuidando que cada una esté a la misma distancia desde el centro de la figura para que resulte un polígono regular.

Observa las imagenes.

Actividad. Crea los siguientes polígonos a partir de su ángulo central.

3 lados, 4 lados, 5 lados, 6 lados y 7 lados. la distancia que debe existir desde el centro hacia cada vértice es de 3 centímetros en todas las figuras.

B2. Actividad 27. 2/12/15

B2. Actividad 27. 2/12/15

Tema. Cálculo de la medida de los ángulos externos de un polígono.

Como el nombre lo indica los ángulos externos de un polígono son los que se forman fuera de su perímetro.

Para hacer el cálculo correcto se debe extender la línea recta de una de las aristas, esto servirá para medir los grados el ángulo externo. 

Recuerda que siempre el ángulo exterior sumado con el ángulo interior sumarán 180 grados.

Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.

Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.


Ejemplos.

Actividad. Construye 10 polígonos irregulares calcule la medida de sus ángulos externos.

B2. Actividad 26. 1/12/15

B2. Actividad 26. 1/12/15

Tema. Cálculo de la medida de los ángulos internos de un polígono.

Como el nombre lo indica los ángulos internos de un polígono son los que se forman dentro de su perímetro.

Para calcular la medida del ángulo debe alinearse la marca del transportador con el vértice y la arista del ángulo que se desea medir.

En caso de que el ángulo sea mayor de 180° simplemente se deben sumar los grados que hacen falta hasta donde se separan las aristas.

Recuerda aplicar el procedimiento que utilizaste para medir ángulos en los segmentos AB, de las actividades anteriores.

Ejemplo.

Actividad. Construye 10 polígonos irregulares  y me de sus ángulos internos.

B2. Actividad 25. 30/11/15

B2. Actividad 25. 30/11/15

Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.